1. Põhivalemi füüsikalise printsiibi kontrollimine
Massi jäävuse seadus
Kõik valemid põhinevad m=ρ×V (mass = tihedus × ruumala) füüsikalisel olemusel.
Tiheduse väärtus
Puhta alumiiniumi teoreetiline tihedus: 2698 kg/m³ (20 ℃)
Ligikaudne väärtus 2700 kg/m³ on tööstusarvutuste jaoks mõistlik (viga < 0,1%).
2. Geomeetriliste valemite ranguse kontrollimine
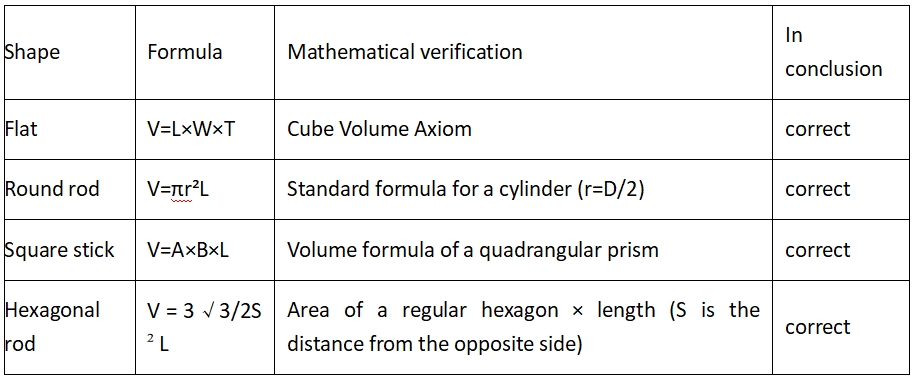
2.1. Standardne geomeetriline ruumala valem
Ruudukujuliste torude valemi piirangud:
See kehtib juhul, kui toru seina paksus on ühtlane ja sisemine nurk on täisnurk (tegelikul ruudukujulisel torul on ümar üleminek ja teoreetiline viga on umbes 1-3%).
3. Ühiku süsteemi järjepidevuse kontrollimine
Üksusteülene arvutus riskipunktide uurimisel
4. Tehnilise sobivuse muudatus
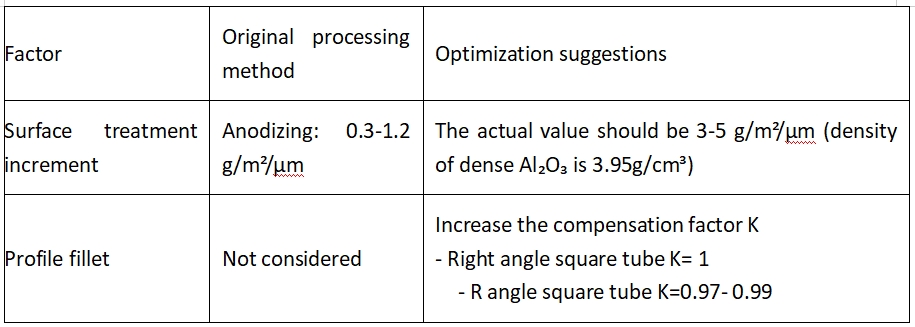
4.1. Mitteideaalsete tegurite kompenseerimine
4.2. Taluvuse mõju kvantifitseerimine
Paksuse tolerants ±10% → Kaalu hälve ±(8% ~ 12%) (õhukese seinaga osad on tundlikumad)
Lahendus: W tegelik = W teoreetiline × (1 + Δt / t) (Δt : paksuse hälve)
5. Piirtingimuse test
Äärmusliku juhtumi kontrollimine:
Tihedusanomaalia stsenaarium
7xxx sulam (7075): Mõõdetud tihedus 2,810 g/cm³ → Kui kogemata kasutatakse tihedust 2,7 g/cm³, on viga +4,1%.
Valemitabel
4t(A + B)- 4t² on standardne inseneriarvutus, mis arvutatakse sektsiooni ümbermõõdu korrutamisel seina paksusega ja seejärel nelja nurga lahutamisel.
Arvutusnäide:
1.6061 alumiiniumplaat(1000 × 500 × 10 mm, pikkus 2 m): L = 1000 × 500 × 2 × 0,0027 = 27 kg
2.7075 ümmargune toru(välisläbimõõt 50 mm, seina paksus 3 mm, pikkus 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Ruudukujuline toru(40 × 40 × 2 mm, pikkus 3 m): W = [2 × 2 × (40 + 40 - 4) × 3] × 0,0027 × 0,98 ≈ 2,42 kg
Soovitatav töövoog
1. Valige tihedus → 2. Mõõtke tegelik suurus → 3. Valige kompensatsioonitegur → 4. Arvutage valemi abil
Postituse aeg: 17. juuni 2025